
Arbre bicolore, arbre avl, skiplist
Description
regroupe 3 petits projets d'algorithmiques classiques : les arbres équilibrés AVL, arbre Bicolore et les SkipList. Chaque projet contient une belle interface graphique.
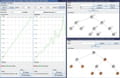
Les AVL et Bicolore : l'interface affiche graphiquement l'arbre. On peut ajouter ou supprimmer des noeuds, l'équilibrage de l'arbre se fait automatiquement. Il est a noté que pour les Bicolores, seule l'insertion est possible. Vous pouvez essayer d'implanter la suppression. L'interface est assez belle et intuitive, elle permet de comprendre aisement le fonctionnement des arbres équilibrés.
Les SkipList : les skiplist sont des listes dont le cout de recherche est en moyenne, linéaire. La recherche est donc optimisée. Le programme Java permet de comparer graphiquement les differences de cout de recherche d'un élement dans une skiplist et dans une linkedlist (liste chainée classique) en fonction de la taille de la liste.
Pour éxecuter/compiler les projets :
chaque projet possede un script Windows compiler.bat et run.bat qui permet de compiler/executer le projet. Sous UNIX, ouvrez ces scripts et regardez les instructions effectuées.
NOTE: dans le zip, seuls les sources JAVA sont présents. Vous devez les compiler. Les sources ont été testés sous JAVA 1.5 sans problème
Bugs connus :
-bug parfois dans l'insertion d'un noeud dans l'arbre bicolore.
Seul bug connu pour le moment... :D
Les AVL et Bicolore : l'interface affiche graphiquement l'arbre. On peut ajouter ou supprimmer des noeuds, l'équilibrage de l'arbre se fait automatiquement. Il est a noté que pour les Bicolores, seule l'insertion est possible. Vous pouvez essayer d'implanter la suppression. L'interface est assez belle et intuitive, elle permet de comprendre aisement le fonctionnement des arbres équilibrés.
Les SkipList : les skiplist sont des listes dont le cout de recherche est en moyenne, linéaire. La recherche est donc optimisée. Le programme Java permet de comparer graphiquement les differences de cout de recherche d'un élement dans une skiplist et dans une linkedlist (liste chainée classique) en fonction de la taille de la liste.
Pour éxecuter/compiler les projets :
chaque projet possede un script Windows compiler.bat et run.bat qui permet de compiler/executer le projet. Sous UNIX, ouvrez ces scripts et regardez les instructions effectuées.
NOTE: dans le zip, seuls les sources JAVA sont présents. Vous devez les compiler. Les sources ont été testés sous JAVA 1.5 sans problème
Conclusion :
Bugs connus :
-bug parfois dans l'insertion d'un noeud dans l'arbre bicolore.
Seul bug connu pour le moment... :D
Codes Sources
A voir également
- Arbre bicolore, arbre avl, skiplist
- Calculer la hauteur d'un arbre ✓ - Forum C / C++ / C++.NET
- Arbre de tournoi - Forum PHP
- Comment dessiner un arbre généalogique - Forum PHP
- Comment dessiner un arbre facilement - Forum Java
- Générateur arbre généalogique - Forum Java


Vous n'êtes pas encore membre ?
inscrivez-vous, c'est gratuit et ça prend moins d'une minute !
Les membres obtiennent plus de réponses que les utilisateurs anonymes.
Le fait d'être membre vous permet d'avoir un suivi détaillé de vos demandes et codes sources.
Le fait d'être membre vous permet d'avoir des options supplémentaires.