
UnitsWV_4: Page Unités (simples)
Contenu du snippet
Bonjour,
Nous arrivons enfin aux unités, alors qu'habituellement, on commence par elles.
Une unité (simple) possède un nom, une symbole et une valeur.
De plus, elle correspond à une dimension qui comporte une ou plusieurs grandeurs.
Nous verrons plus tard les unités composées.
Le code source du logiciel "UnitsWV" est disponible dans:
CodeS-SourceS: UnitsWV: Dimensions, grandeurs et unités (SI*).
Il faut bien sûr prendre garde de suivre l'ordre des symboles correspondants Φ, Ω, M, T, I, Θ, N, J, C.
Une unité basique est donc de la forme radᵉ¹·srᵉ²·mᵉ³·kgᵉ⁴·sᵉ⁵·Aᵉ⁶·Kᵉ⁷·molᵉ⁸·cdᵉ⁹·¤ᵉ¹⁰ (avec ᵉⁱ: exposants entiers).
Comme les termes avec un exposant nul peuvent être supprimés, on peut sans ambigüité confondre les unités de base avec l'élément de 𝔹¹⁰ correspondant.
Par exemple: kg = rad°·sr°·m°·kg¹·s°·A°·K°·mol°·cd°·¤°.
Exemples:
rad: radian ⇄ Φ: {angle}
sr: stéradian ⇄ Ω: {angle solide}
m: mètre ⇄ L: {longueur}
kg: kilogramme ⇄ M: {masse}
s: seconde ⇄ T: {temps}
A: ampère ⇄ I: {courant électrique}
K: kelvin ⇄ Θ: {température}
mol: mole ⇄ N: {quantité de matière}
cd: candela ⇄ J: {intensité lumineuse}
¤: unité monétaire ⇄ C: {devise}
m²: ⇄ L²: {aire}
m·s⁻¹: ⇄ L▫T⁻¹: {vitesse}
m·s⁻²: ⇄ L▫T⁻²: {accélération}
rad·s⁻¹: ⇄ Φ▫T⁻¹: {vitesse angulaire}
m·kg·s⁻² = N: newton ⇄ L▫M▫T⁻²: {force}
m²·kg·s⁻² = J: joule ⇄ L²▫M▫T⁻² {travail}
m²·kg·s⁻³ = W: watt ⇄ L²▫M▫T⁻³ {puissance}
Certaines éléments de 𝔹¹⁰ (parmi ceux dont les exposants respectifs correspondent à des dimensions nommées) ont des noms spécifiques, comme par exemple le Newton:
N = rad°·sr°·m¹·kg¹·s⁻²·A°·K°·mol°·cd°·¤° = m·kg·s⁻²
correspond à L▫M▫T⁻²: {force}
L'opération · de multiplication des unités basiques correspond celles des grandeurs, et donc à celle des dimensions:
Le produit d'unités basiques est égal à l'unité basique du produit des dimensions correspondantes.
Définissons maintenant le groupe des valeurs de grandeur 𝕍ⁿ = ℝ×𝔹ⁿ:
(r,𝓾)∗(r',𝓾') = (rr')∗(𝓾∘𝓾') ou r𝓾 * r'𝓾' = rr'𝓾𝓾'
1 = (1,𝟙) (élément neutre)
Simplification d'écriture: (r,𝓾), (1,𝓾), (r,𝟙), sont souvent notés r𝓾, 𝓾, r respectivement.
Nous pouvons confondre le groupe des unités basiques 𝔹ⁿ et le sous-groupe des éléments de 𝕍ⁿ dont la valeur réelle est égale à 1 (r=1).
Pour obtenir une structure algébrique, définissons encore l'addition:
Pour chaque sous-ensemble de 𝕍ⁿ ayant la même unité, on définit la somme en utilisant l'addition héritée des réels:
(r,𝓾) + (r’,𝓾) = (r+r',𝓾) ou r𝓾 + r'𝓾 = (r+r')𝓾
avec l'élément neutre: 0 = (0,𝓾).
Le calcul avec les valeurs de grandeurs est conforme au calcul algébrique habituel.
Comme de bien entendu, les deux éléments neutres (0 pour l'addition et 1 pour la multiplication) sont uniques !!!
Essayer de donner une signification "non neutre" (ou "utile") à l'un ou l'autre est contraire au calcul algébrique !!!
De plus, donner plusieurs noms à un élément unique ne peut qu'"embrouiller" les choses.
Elle peut être triée selon les symboles (⇓ de gauche) ou selon les noms (⇓ de droite).
La zone de spécification indique:
‥ La valeur en unité basique.
L'affichage de l'éventuel nom de l'unité basique est en préparation
‥ L'unité SI (si elle est dérivée d'un angle, rad ou sr sont toujours indiqués).
‥ Les préfixes possibles.
‥ La dimension de l'unité.
Contrairement aux pages Dimensions et Grandeurs, les zones Unités de même dimension et Grandeurs de même dimension ne tiennent pas compte des neutralisations éventuelles d'unités de base, car les unités sont principalement liées à une dimension "complète".
En effet, selon le "principe" suivant:
lorsqu'un terme est considéré comme utile dans une expression, elle doit aussi être considérée comme utile dans toute composition de ce terme.
Exemple: Considérons la formule
M = P/ω ou moment d'une force = puissance / vitesse angulaire
avec les unités SI:
M en m²·kg·s⁻²
P en W = J/s = N·m/s = m²·kg·s⁻³
ω en rad·s⁻¹.
Avec des valeurs, on a par exemple
1 m²·kg·s⁻² = 1 W / 1 rad·s⁻¹ = 1 m²·kg·s⁻³ / 1 rad·s⁻¹ = 1 rad⁻¹·m²·kg·s⁻²
Bonne lecture et agréable utilisation …
CodeS-SourceS: UnitsWV_0: Parties communes
CodeS-SourceS: UnitsWV_1: Page Base
CodeS-SourceS: UnitsWV_2: Page Dimensions
CodeS-SourceS: UnitsWV_3: Page Grandeurs
Brochure sur le SI: Le Système international d'unités
SI Brochure: The International System of Units (SI)
Vocabulaire international de métrologie
Métrologie française: Les unités de mesure
METAS: Unités de mesure
Wikipédia: Unité de mesure
WikipédiA: Système international d'unités
WikipediA: International System of Units
WikipediA: Internationales Einheitensystem
NIST: International System of Units
Nous arrivons enfin aux unités, alors qu'habituellement, on commence par elles.
Une unité (simple) possède un nom, une symbole et une valeur.
De plus, elle correspond à une dimension qui comporte une ou plusieurs grandeurs.
Nous verrons plus tard les unités composées.
Le code source du logiciel "UnitsWV" est disponible dans:
CodeS-SourceS: UnitsWV: Dimensions, grandeurs et unités (SI*).
Unités basiques
En nous reportant à la construction de 𝔻ⁿ, 𝔻⁷ et 𝔻¹⁰ de UnitsWV_2: Page Dimensions, bâtissons maintenant le groupe des unités basiques 𝔹¹⁰ généré par les symboles d'unités de base rad, sr, m, kg, s, A, K, mol, cd, ¤.Il faut bien sûr prendre garde de suivre l'ordre des symboles correspondants Φ, Ω, M, T, I, Θ, N, J, C.
Une unité basique est donc de la forme radᵉ¹·srᵉ²·mᵉ³·kgᵉ⁴·sᵉ⁵·Aᵉ⁶·Kᵉ⁷·molᵉ⁸·cdᵉ⁹·¤ᵉ¹⁰ (avec ᵉⁱ: exposants entiers).
Comme les termes avec un exposant nul peuvent être supprimés, on peut sans ambigüité confondre les unités de base avec l'élément de 𝔹¹⁰ correspondant.
Par exemple: kg = rad°·sr°·m°·kg¹·s°·A°·K°·mol°·cd°·¤°.
Exemples:
rad: radian ⇄ Φ: {angle}
sr: stéradian ⇄ Ω: {angle solide}
m: mètre ⇄ L: {longueur}
kg: kilogramme ⇄ M: {masse}
s: seconde ⇄ T: {temps}
A: ampère ⇄ I: {courant électrique}
K: kelvin ⇄ Θ: {température}
mol: mole ⇄ N: {quantité de matière}
cd: candela ⇄ J: {intensité lumineuse}
¤: unité monétaire ⇄ C: {devise}
m²: ⇄ L²: {aire}
m·s⁻¹: ⇄ L▫T⁻¹: {vitesse}
m·s⁻²: ⇄ L▫T⁻²: {accélération}
rad·s⁻¹: ⇄ Φ▫T⁻¹: {vitesse angulaire}
m·kg·s⁻² = N: newton ⇄ L▫M▫T⁻²: {force}
m²·kg·s⁻² = J: joule ⇄ L²▫M▫T⁻² {travail}
m²·kg·s⁻³ = W: watt ⇄ L²▫M▫T⁻³ {puissance}
Certaines éléments de 𝔹¹⁰ (parmi ceux dont les exposants respectifs correspondent à des dimensions nommées) ont des noms spécifiques, comme par exemple le Newton:
N = rad°·sr°·m¹·kg¹·s⁻²·A°·K°·mol°·cd°·¤° = m·kg·s⁻²
correspond à L▫M▫T⁻²: {force}
L'opération · de multiplication des unités basiques correspond celles des grandeurs, et donc à celle des dimensions:
Le produit d'unités basiques est égal à l'unité basique du produit des dimensions correspondantes.
Valeur d'une grandeur
Soient r,r'∊ℝ (réels) et 𝓾,𝓾'∊𝔹ⁿ (groupe des unités basiques).Définissons maintenant le groupe des valeurs de grandeur 𝕍ⁿ = ℝ×𝔹ⁿ:
(r,𝓾)∗(r',𝓾') = (rr')∗(𝓾∘𝓾') ou r𝓾 * r'𝓾' = rr'𝓾𝓾'
1 = (1,𝟙) (élément neutre)
Simplification d'écriture: (r,𝓾), (1,𝓾), (r,𝟙), sont souvent notés r𝓾, 𝓾, r respectivement.
Nous pouvons confondre le groupe des unités basiques 𝔹ⁿ et le sous-groupe des éléments de 𝕍ⁿ dont la valeur réelle est égale à 1 (r=1).
Pour obtenir une structure algébrique, définissons encore l'addition:
Pour chaque sous-ensemble de 𝕍ⁿ ayant la même unité, on définit la somme en utilisant l'addition héritée des réels:
(r,𝓾) + (r’,𝓾) = (r+r',𝓾) ou r𝓾 + r'𝓾 = (r+r')𝓾
avec l'élément neutre: 0 = (0,𝓾).
Le calcul avec les valeurs de grandeurs est conforme au calcul algébrique habituel.
Comme de bien entendu, les deux éléments neutres (0 pour l'addition et 1 pour la multiplication) sont uniques !!!
Essayer de donner une signification "non neutre" (ou "utile") à l'un ou l'autre est contraire au calcul algébrique !!!
De plus, donner plusieurs noms à un élément unique ne peut qu'"embrouiller" les choses.
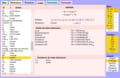
UnitsWV: page Unités
La liste Unités affiche les unités simples qui correspondent aux couples (grandeur: unité) de base actifs et qui font partie d'au moins une famille sélectionnée.Elle peut être triée selon les symboles (⇓ de gauche) ou selon les noms (⇓ de droite).
La zone de spécification indique:
‥ La valeur en unité basique.
L'affichage de l'éventuel nom de l'unité basique est en préparation
‥ L'unité SI (si elle est dérivée d'un angle, rad ou sr sont toujours indiqués).
‥ Les préfixes possibles.
‥ La dimension de l'unité.
Contrairement aux pages Dimensions et Grandeurs, les zones Unités de même dimension et Grandeurs de même dimension ne tiennent pas compte des neutralisations éventuelles d'unités de base, car les unités sont principalement liées à une dimension "complète".
En effet, selon le "principe" suivant:
lorsqu'un terme est considéré comme utile dans une expression, elle doit aussi être considérée comme utile dans toute composition de ce terme.
Exemple: Considérons la formule
M = P/ω ou moment d'une force = puissance / vitesse angulaire
avec les unités SI:
M en m²·kg·s⁻²
P en W = J/s = N·m/s = m²·kg·s⁻³
ω en rad·s⁻¹.
Avec des valeurs, on a par exemple
1 m²·kg·s⁻² = 1 W / 1 rad·s⁻¹ = 1 m²·kg·s⁻³ / 1 rad·s⁻¹ = 1 rad⁻¹·m²·kg·s⁻²
Code de la page Unités
//// U.js: Unités
function U() {}
U.U=new Array(0);
U.Ini=function() {
U.uu=new Array(nbU); U.nn=new Array(Lng.mes.length);
U.sel=null; U.su=-1; U.cln=0; U.iv=false;
var i=0; do U.uu[i]=i; while (++i<nbU);
U.uu.sort(U.CpS);
};
U.Lng=function() {S.SoN(U.nn,U.U); U.Lst(U.cln);};
U.Lst=function(n) {
var b=false,i=0,k,s='',uu=U.U[Lng.sel];
U.k=(n==0)?U.uu:U.nn[Lng.sel];
do {k=U.k[i];
if ((U.Fml(k)==0)||!U.Bas(k)) continue;
if (k==U.su) {b=true; z="lS' id='us";} else z="lN";
s+="<div class='"+z+"' onclick='U.Clk(this,"+k+")'>"+U.s[k]
+"<span style='float:right; width:144px'>"+uu[k]+"</span></div>";
} while (++i<nbU);
document.getElementById('Z4a').innerHTML=s; U.cln=n;
document.getElementById('usa').style.backgroundColor=colSel[1-n];
document.getElementById('usb').style.backgroundColor=colSel[n];
if (b) U.sel=document.getElementById('us'); else {U.sel=null; U.su=-1;}
U.Upd();
};
U.Upd=function() {
if (U.sel==null) {document.getElementById('Z4b').innerHTML='';
document.getElementById('Z4c').innerHTML='';
document.getElementById('Z4e').innerHTML='';
document.getElementById('Z4g').innerHTML=''; return;}
var uu=U.U[Lng.sel],qq=Q.Q[Lng.sel];
var d=U.d[U.su],u=D.TxU(D.b[d]),i,s,v=U.v[U.su],vv=1.0/v;
var mm=Lng.mes[Lng.sel];
document.getElementById('Z4b').innerHTML="<b>"+uu[U.su]+"</b>";
s="<p style='height:20px; text-align:center'>1 "+U.s[U.su]+" = "+v.si()+" "+u
+"</p>"+"<p style='height:20px; text-align:center'>1 "+u+" = "+vv.si()+" "
+U.s[U.su]+"</p><p> </p>"+"<p style='height:20px'>"+mm[10]
+":<span style='float:right; width:360px'>"+U.Pfx(U.su)+"</span></p>"
+"<div style='float:left; height:20px; width:110px'>"
+mm[17]+":</div><div style='float:left; width:160px'>{"
+D.D[Lng.sel][d]+"}</div><div style='float:left; color:blue'>"
+D.TxQ(D.b[d])+"</div></div>";
document.getElementById('Z4c').innerHTML=s;
for (i=0,s='';i<nbU;i++)
if (U.Bas(k=U.k[i])&&(d==U.d[k])&&(k!=U.su)&&(U.Fml(k)!=0))
s+="<div style='overflow:hidden'>"+uu[k]
+"<span style='float:right; width:232px'>1 "
+((U.iv)?(U.s[k]+" = "+(U.v[k]/v).si()+" "
+U.s[U.su]):(U.s[U.su]+" = "+(v/U.v[k]).si()+" "
+U.s[k]))+"</span></div>";
document.getElementById('Z4e').innerHTML=s;
for (i=0,s='';i<nbQ;i++)
if (d==Q.d[k=Q.k[i]])
s+="<div style='overflow:hidden'><span style='font-size:10px'>"+Q.i[k]
+"</span><span style='float:right; width:400px'>"+qq[k]+"</span></div>";
document.getElementById('Z4g').innerHTML=s;
};
U.CpS=function(aa,bb) { // compare symbols
var a=U.s[aa].toLowerCase(),b=U.s[bb].toLowerCase();
if (a<b) return -1; if (a>b) return 1; return 0;
};
U.Clk=function(e,k) {
if (U.sel!=null) U.sel.className='lN';
e.className='lS'; U.sel=e; U.su=k; U.Upd();
};
U.Inv=function() {U.iv=!U.iv; U.Upd();};
U.Pfx=function(n) {
var b,i,s='',p=U.p[n];
if (p==0) return '-';
for (i=0,b=1;i<nbP;i++,b<<=1) if ((p&b)!=0) s+=((s!='')?', ':'')+B.p[i];
return s;
};
U.Bas=function(k) {var e=D.de[U.d[k]]; return ((e&bas)==e);}; // Unité ∈ base
U.Fml=function(k) {return fml&U.f[k];}; // Unité dans une famille
Bonne lecture et agréable utilisation …
Liens
CodeS-SourceS: UnitsWV: Dimensions, grandeurs et unités (SI*) (avec le Zip 17.5.2018)CodeS-SourceS: UnitsWV_0: Parties communes
CodeS-SourceS: UnitsWV_1: Page Base
CodeS-SourceS: UnitsWV_2: Page Dimensions
CodeS-SourceS: UnitsWV_3: Page Grandeurs
Brochure sur le SI: Le Système international d'unités
SI Brochure: The International System of Units (SI)
Vocabulaire international de métrologie
Métrologie française: Les unités de mesure
METAS: Unités de mesure
Wikipédia: Unité de mesure
WikipédiA: Système international d'unités
WikipediA: International System of Units
WikipediA: Internationales Einheitensystem
NIST: International System of Units
Compatibilité : 11 juillet 2018


Vous n'êtes pas encore membre ?
inscrivez-vous, c'est gratuit et ça prend moins d'une minute !
Les membres obtiennent plus de réponses que les utilisateurs anonymes.
Le fait d'être membre vous permet d'avoir un suivi détaillé de vos demandes et codes sources.
Le fait d'être membre vous permet d'avoir des options supplémentaires.